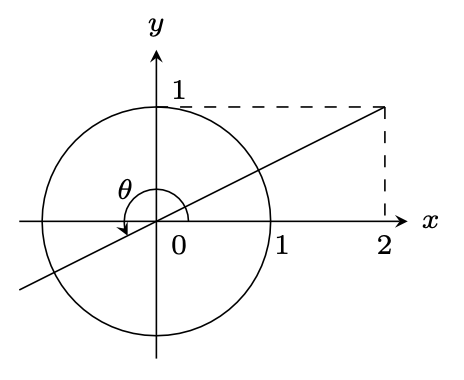
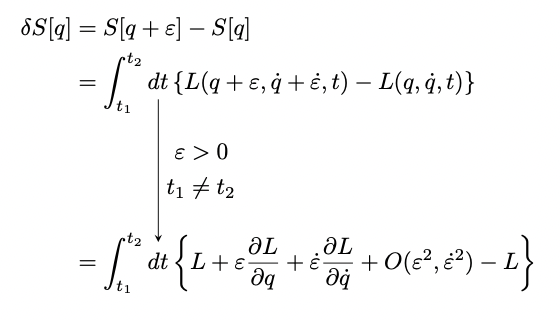次の例では、日本語のテキストを使ったTikZ図の作り方を紹介します。 LuaLaTeXで luatexjaパッケージ を使ってます。pTeXよりはちょっと遅いけど、計算にLuaの機能をよく使うので便利なんですよね。それに、luatexjaなら standaloneクラス でも日本語がちゃんと使えるのが嬉しいところ。 — LaTeX.org (@TeXgallery) December 16, 2025
https://t.co/V0AU3vracq https://t.co/sEvdrKKweD pic.twitter.com/92znuQ9mID — LaTeX.org (@TeXgallery) March 5, 2025 \documentclass[tikz,border=50pt]{standalone}% https://tikz.jp/dora/ \usetikzlibrary{shapes.callouts} \begin{document} \begin{tikzpicture}[draw, line width=1pt, even odd rule, xscale=-1] % body \filldraw[fill=blue!30] (1.2,-5) to[out=290,…
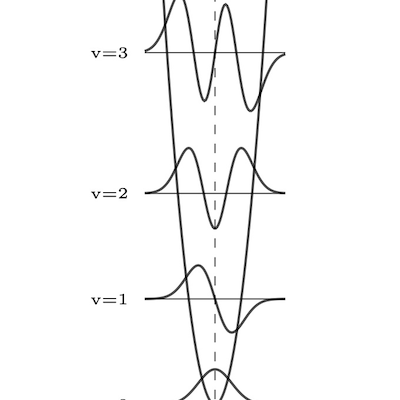
図は、調和振動子の最初の4つの振動状態を、波動関数によって示したものです。 pgfplotsは良い選択です。 pic.twitter.com/E6j5L24BG6 — LaTeX.org (@TeXgallery) February 17, 2025
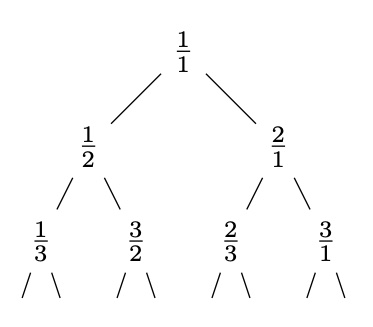
X/Twitterで、こちらの投稿を@884_96さんによって見かけました。 やっぱこれすごいなあ pic.twitter.com/2NG8JFyUb1 — 林 俊介 (@884_96) January 11, 2025 (4) の木構造が気に入ったので、素早くこの図を作成しました:
Here’s the Japanese translation for your detailed description: PGFplots.netの開始後、私はpgfplotsでさらに実験をしました。私がいつものように各グラフィックソフトウェアで行うように、フラクタルをどのように表現できるか、そしてそれによって有用または興味深い側面があるかどうかを考えました。ここでは速度やメモリスペースは二次的なもので、時間とともに容量は変わります。 私が興味を持っているのは、例えば
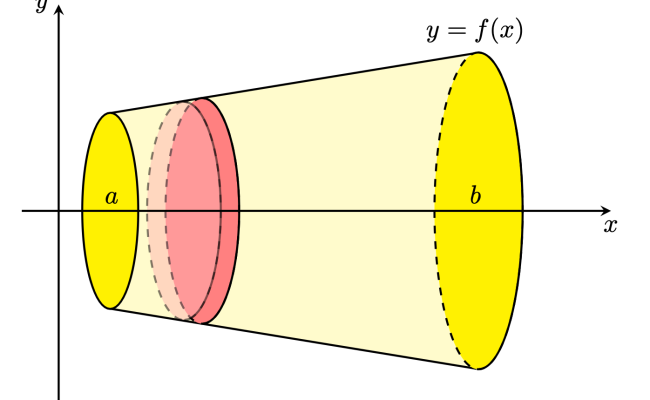
私はフラクタル風景を生成し、LaTeXなどで利用可能な機能を活用したいと考えています。 アプローチ: Luaを使用してダイヤモンド・スクエア・アルゴリズムによる風景の計算 pgfplotsを使用して出力することで、多様な表示オプションが利用できる メッシュを使用したサーフェスプロット Colormapを使用して色付けを行う:海面下は青、山は緑、雪は白、高度によって色が変わる
リンデンマイヤーシステム、通称L-システムは、「置換システム」です:ある(グラフィック)オブジェクトの部分が、最も単純な場合にはその縮小されたオブジェクト自体に置き換えられます。これが繰り返され、例えば再帰的に行われます。これにより、非常に複雑なフラクタル構造が生まれ、同時に非常にシンプルに定義されることがあります。 最も単純な例はコッホ曲線で、スノーフレーク曲線とも呼ばれます。知らない人は、Wikipediaのリンクをフォローしてください。:-) ここでは説明するつもりはありませんが、TikZを使って最も簡単に生成する方法を簡単に示します。
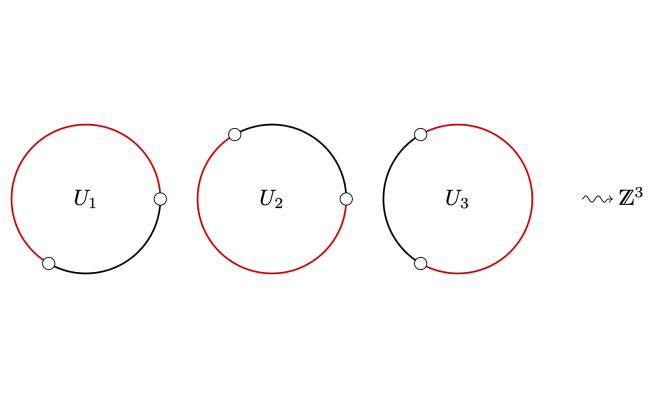
ここでは、繰り返し関数システム、略してIFSについて扱います。ここでは繰り返し変換が行われます。空間が何度も自分自身にマッピングされます。このプロセスにはさまざまなマッピング規則があり得ます。理想的にはこれを無限に行い、すべての間で不変である空間内の集合を考察します。この集合はフラクタルになる可能性があります! 理論はさておき、Wikipediaで基本的な内容を、そして素晴らしい本でより深く理解することができます。では、これをどのように生成するのでしょうか? 最も簡単な方法は「カオスゲーム」と呼ばれるものです。一点を取り、その点に一つの変換を適用します。変換によって不変である点集合に関わるため、目的の点は集合内に落ちなければなりません。この新しい点でプロセスを繰り返し、何千回も繰り返して図が浮かび上がるまで続けます。